Page 387 - MORPHOLOGIE DES STRUCTURES

www.academieroyale.be

LES PORTIQUES 387

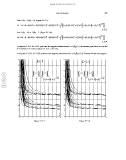
Pour L h1 = H h2 = 10 (figure 2.15.3.) :

W = 10Z + (1 +1 k ) H L + 20(Z k)(H L )2 + (2 k )( H L )3 + 3 (Ω2 Ω1 )(L H )2 + 2 ( H )  ( Ω3 ) 1+ ( L )2 3 2  
1   
 L + Ω2 H   .



2.15.3.

Pour L h1 = 10 et H h2 = 5 (figure 2.15.4.) :

W = 10Z + (1 + 1 k ) H L + 10 (Z k)(H L)2 + (2 k )(H L )3 + 3 (Ω2 Ω1 )(L H )2 + 2(H L )  + ( Ω 2 Ω3 ) 1+ (L H )2 3 2  .
1  
  

2.15.4.

Les figures 2.15.5. à 2.15.22. précisent les rapports adimensionnels σ Ω ( p1L ) nécessaires pour tracer les courbes

de l’indicateur de volume (figures 2.15.3. et 2.15.4.).

Les figures 2.15.23. à 2.15.28. précisent les rapports adimensionnels σ Ω4 ( p1L) de l’éventuel tirant entre appuis.

20 L = H =10 20 L =10; H = 5
W h1 h2 W h1 h2

18 18

16 16

14 14 L
1 L 1 H 1 H 1 H
W W+ L 3 + 2 + 2Ω2 1+ 2 3/ 2 H + k L W W+ L 3 + 2+ 2 Ω2 1+ 2 3/2 + k L
Ω2 Ω2
L L

Ω1 H Ω3 H Ω1 H Ω3 H

12 12

10 10 k =1
2
86 4 2 k =1 1086 4

10 ∞

8∞ 8
7.5
7.5

Z =0.75 Z =0.75

6 6 k =1

84 2 k =1 2
10 6 18064
∞
∞

4 10 4
∞ 86 4 3.75
3.75 2 k =1 Z =0.375 ∞ 10 8 6 4 2 k =1 Z =0.375
Z =0.25 2.5 Z =0.25
2.5 2
2

LL

HH
00

0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10

Figure 2.15.3. Figure 2.15.4.